


Next: About this document ...
Up: Abstracts of the presentations
Previous: Stefan Müller
Asymptotic self-similarity in a model of branching in microstructured
materials
This talk addressed some properties of a scalar 2D model which has been
proposed to describe microstructure in martensitic phase transformations,
consisting in
minimizing the bulk energy
where 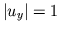 a.e. and
a.e. and 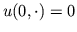 .
Kohn and Müller [R. V. Kohn and S. Müller, Comm. Pure and Appl. Math.
47, 405 (1994)] proved the existence of the minimizers for
.
Kohn and Müller [R. V. Kohn and S. Müller, Comm. Pure and Appl. Math.
47, 405 (1994)] proved the existence of the minimizers for
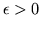 ,
and obtained bounds on the total energy which suggested
self-similarity of the minimizer. Building upon their work, we derive a
local upper bound on the energy and on the minimizer itself, and show that
the minimizer
,
and obtained bounds on the total energy which suggested
self-similarity of the minimizer. Building upon their work, we derive a
local upper bound on the energy and on the minimizer itself, and show that
the minimizer 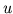 is asymptotically self-similar, in the sense that the
sequence
is asymptotically self-similar, in the sense that the
sequence
(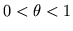 )
has a strongly converging subsequence in
)
has a strongly converging subsequence in 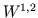 .
.